Her vil det etterhvert komme beskrivelse av de fleste av demonstrasjonsfors?kene vi skal gj?re i l?pet av semesteret.
Tyngden av vannet i et kar, og den hydrostatiske trykkrafta som virker p? bunnflaten i karet (5. mars og diverse ganger til)
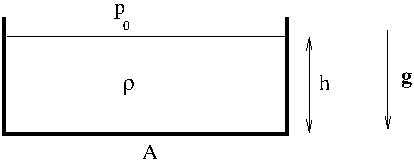
Et kar med grunnflate \(A\) er fyllt opp med vann til en h?yde \(h\). Vannet har tetthet \(\rho\). Lufta har trykk \(p_0\). Tyngdens akselerasjon \(\mathbf{g}\) virker ned.
Vis hvordan vannets tyngde er relatert til trykkrafta som virker fra vannet p? bunnflaten.
Hint: Vannets tyngde er volumintegralet av \(\rho \mathbf{g}\), dvs. vannets tyngde er lik \(\rho \mathbf{g} A h\). I vannet har vi hydrostatisk trykk \(p = p_0 - \rho g z\), hvor vi har implisert at \(z=0\) i vannoverflaten og \(z\)-aksen peker oppover. Det hydrostatiske trykket p? bunnen av karet er \(p = p_0 + \rho g h\). Trykkrafta som virker p? bunnflaten blir dermed \((p_0 + \rho g h)A \mathbf{n}\), hvor vi har latt symbolet \(\mathbf{n}\) bety en enhetsvektor som peker nedover. Dersom det ikke hadde v?rt vann i karet hadde trykket like over bunnflaten v?rt lufttrykket \(p_0\), og da hadde trykkrafta som virket p? bunnflaten ha v?rt \(p_0 A \mathbf{n}\). Dermed ser vi at vannets tyngde er lik differansen mellom trykkrafta som virker p? bunnflaten i karet med og uten vann. Dette er et faktum vi benytter oss av nesten hver gang vi bruker en kj?kkenvekt!
Hydrostatisk trykk i opp-ned glass over kar med vann (19.januar)

Figuren viser ei sk?l (S) og et glass (G). Glasset holdes med bunnen (B) opp og med ?pningen ned, p? en slik m?te at det ikke er kontakt mellom glasset og sk?la. I sk?la og i glasset er det vann med tetthet \(\rho\). Utenfor glasset er vannet i kontakt med luft i en h?yde \(h\) over sk?las bunn. Inni glasset n?r vannet helt opp til glassets bunn (B) i en h?yde \(H\) over sk?las bunn. Tyngdens akselerasjon \(g\) er rettet ned. Lufta har konstant trykk \(p_0\). Sk?la har en flat bunn med areal \(A\).
Regn ut trykket \(p\) p? et vilk?rlig sted i vannet!
Hydrostatisk trykk i opp-ned glass fyllt med vann og med l?st lokk under (19.januar)

Glasset G er fyllt med vann med tetthet \(\rho\). Under glasset har vi et l?st lokk L med masse \(m\). Under lokket har vi luft med trykk \(p_0\). Glassets ?pning har tverrsnitt med areal \(A\). Lokket faller ikke ned selv om det er vann over og luft under!
Regn ut trykket \(p\) p? et vilk?rlig sted i vannet inni glasset! Merk at svaret ikke er entydig, vi kan kun si at trykket p? et vilk?rlig sted m? v?re mellom en viss minste og st?rste grenseverdi. Finn disse grenseverdiene!
Hevert: T?mme vann fra et kar ved hjelp av en plastslange (19.januar)
Detter er i praksis oppgave 9 i kapittel 10. Vi gjorde eksperimentet ved ? la A v?re et lite glass og C v?re en st?rre b?tte: Vi t?mte det lille glasset uten ? helle med glasset p? skr?.

Dette er en typisk anvendelse for Bernoullis likning i kapittel 10 i kompendiet!
Airbrush (19.januar)
Dette er et eksperiment man kan gj?re med et suger?r og litt tape. Se beskrivelse i Wikipedia om "Atomizer nozzle" http://en.wikipedia.org/wiki/Atomizer_nozzle
Relevant teori l?rer vi om i kapittel 10 i kompendiet!
Referanser
F?lgende referanser g?r s? dypt i detalj at det ikke anses som pensum ? ha lest dem:
Nettsidene til MUSE (More Understanding with Simple Experiments) hos EPS (European Physical Society)